branch and bound

(보기 문제)퇴각 검색과 분기와 한정의 비교

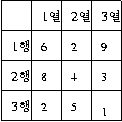
한 행에서 하나의 숫자를 택할 수 있는 문제에서 각 행에서 숫자를 뽑을 때 가장 최소로 뽑는 방법은? 단, 같은 열에서 두 개의 숫자를 뽑을 수는 없다.

위 보기로 두 가지 방법에 대해 알아 보도록 하자.

퇴각 검색(backtracking)

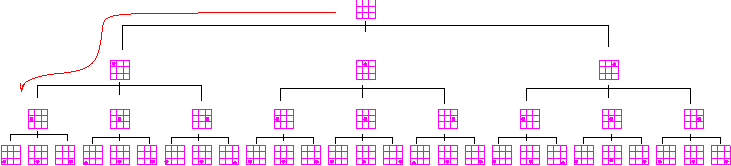
그래프 방문에서 기계적으로 깊이우선탐색을 사용. 재귀호출을 이용함으로 프로그램이 간단.

분기와 한정(branch and bound)

그래프 방문에서 너비우선탐색을 사용하여 1.1 1.2 1.3 1.4 를 방문 후 네 개 중에서 가장 가능성이 있는 것 부터 검색하는 방법을 채택.
이의 구현을 빠르게 하기 위하여 최대 heap 혹은 최소 heap 을 사용한다.
큐, heap 등을 사용하여 구현하므로 프로그램이 되추적과 비교하여 복잡.

한계값(bound)이란?

이 시점에서 나올수 있는 가장 최선의 값을 말한다. 최적화 문제에서는 두가지 방법다 (현재까지 구한값 + 한계 값) 과 (현재까기 구한 답)을 비교하여 가능성이 없으면 미리 잘라버려 속도를 높이는 방법을 택한다.
한계값 의 이해
(보기 1) 미로 찾기 문제에서 가장 빠른 길을 찾기 위한 방법으로 모든길을 다 검사해 보는 방법으로 간다고 하자.(물론 효율적인 방법은 아님)

그림(a)와 같이 가보니 거리는 15 였다.
그림(b)형태로 쥐가 왔다가 할 때 현재까지 온 거리는 6 이다.
그림(c)에서 3 행 2 열에서 도착지갈수 있는 가장 빠른 길은 12 다.

그림(b)와 같은 경로를 채택할 때는 더 이상 길을 가봤자 의미가 없다는 것을 안다. 즉 3 행 2 열 지점에서의 한계값은 12 라고 말한다.

(보기 2)
한 행에서 하나의 숫자를 택할 수 있는 문제에서 각 행에서 숫자를 뽑을 때 가장 최소로 뽑는 방법은? 단, 같은 열에서 두 개의 숫자를 뽑을 수는 없다.
   1   2   3
-------------
   6   2   9
   8   3   4
   7   5   3
   
시작시점에서의 한계값?

1 행에서의 최소는 min{6,2,9} = 2
2 행에서의 최소는 min{8,3,4} = 3
3 행에서의 최소는 min{7,5,3} = 3

이 문제에서는 2+3+3=8 보다 답이 더 작을 수는 없다. 즉 8 이 시작시점에서의 한계값이다. 물론 8 이 답은 아니다.
만약 1 행에서 2 렬을 택하였다면 한계값은 얼마일까?

2 행 3 행에서 2 렬을 다시 선택할 수는 없으므로 2 렬을 제외한 행 중에서 최소 값은
2 행 min{8,4}=4
3 행 min{7,3}=3
4+3=7 이 한계값이다.

만약 현재까기 구한 답이 8 이었다고 하자. 2(현재까지구한값) + 7(한계값) 는 9 이다. 즉 이를 더 이상확장해 보았자 8 보다 더 작을수는 없으므로 더 이상 전진할 필요가 없이 잘라 버린다.

퇴각 검색과 분기와한정 따라가기

퇴각 검색

최초 한계값 8 ,최소값(현재까기 구한답): 무한대

1 행에서 1 열을 선택하면 , 현재 값(6) + 한계값(3+3) 즉 12  12 보다 무한대가 작으므로 다음 단계
  2 행에서   1 열은 안되고 2 렬 선택 현재값(6+3) + 한계값(3) 즉 12 12 보다 무단대가 작으므로 다음 단계
    3 행에서 1,2 렬은 안되고 3 열 선택(마지막) 현재값(6+3+3)=12 , 최소값보다 작으므로 현재까지의 답 12
  2 행에서 3 열을 선택하면 ,  현재값(6+4) + 한계값(5)=15 이 수는 현재까지의 답 12 보다 크므로 가능성 없음

1 행에서 2 열을 선택하면 , 현재값(2) + 한계값(4+3)=9 이므로 가능성 있음 
  2 행에서 1 열을 선택하면 , 현재값(2+8) + 한계값(3)=13 이므로 가능성 없음
  2 행에서 3 열을 선택하면 , 현재값(2+4) + 한계값(7)=13 이므로 가능성 없음


1 행에서 3 열을 선택하면 , 현재 값 9 + 한계값 (3+5)=17  이 값은 현재까지 구한답 13 보다
크므로 더 이상 전진할 필요가 없다.

분기와 한정

최초 한계값 8 , 최소 값 : 무한 대

1행에서 1,2,3렬을 선택
----------------------
1 행에서 1 열을 선택할 때: 현재값(6)+ 한계값(3+3)=12
1 행에서 2 열을 선택할 때: 현재값(2)+ 한계값(4+3)=9
1 행에서 3 열을 선택할 때: 현재값(9)+ 한계값(3+5)=17

세가지 경우중에서 가장 최소값을 가지는 경우는 1 행에서 2 렬을 선택하는 경우이므로
1 행에서 2 렬을 선택 후

2 행에서 1 열과 3 열을 선택 
---------------------------
2 행에서 1 열을 선택할 때: 현재값(2+8)+한계값(3)=13
2 행에서 3 열을 선택할 때: 현재값(2+4)+한계값(7)=13

1 행에서 1 열을 선택하는 경우가 12 로 최소 이므로 
----------------------
2행에서 2 열과 3 열을 선택 

2행에서 2 열을 선택할 때:  현재값(6+3)+한계값(3)=12
2행에서 3 열을 선택할 때:  현재값(6+4)+한계값(5)=15

-------------
2 행에서 2 열을 선택하는 경우  12 가 최소이므로

3 행에서 3 열을 선택하는 경우 : 현재값(6+3+3)=12 즉 현재까지 최소값 12

출처:dovelet

[질/답]

[홈으로] [뒤 로]

[푼 후(0)]