문서 I

참고 자료 프리젠테이션 문서

Indexed Tree

인덱스트리는 이진트리로 구성한 부모노드가 자식노드의 대표가 되게 하는 자료구조이다. 쉽게 말해서, 조건에 맞추어 쭉쭉 올려주는 트리라고 생각하면 된다.

예를 들어보자. 

<문제>
당신은 새로운 계산기 M_Int를 만들려고 한다. 당신은 M_Int에 다음과 같은 기능을 갖게 하려고 한다.
1. 처음에 n과 n개의 수 a[0]~a[n-1]가 입력된다. (n<=100000, n개의 수는 int범위)
2. 명령 개수 T가 입력된다. (T<=100000)
3. 0 x y가 들어오면 a[x]~a[y]의 최솟값을 출력한다.
4. 1 x y가 들어오면 a[x]를 y로 고친다.
M_Int를 구현해보아라. 단, M_Int는 제한 범위 내에 있는 어떤 데이터라도 1초 안에 계산되어야한다.

입력

4
2 4 6 8
4
0 0 2
0 1 2
1 3 1
0 0 3

출력

2
4
1
※생각해보기

1. 나는 인덱스트리를 몰라요 ㅋ

이러한 경우는 단순히 생각할 것이다. 1 x y가 들어오면 간단히 상수시간 내로 연산이 가능하겠지만, 0 x y에서 많은 시간을 소요하게 될 것이다. 다음과 같은 예제를 보면 단순히 생각하던 이들이 깨달음을 얻으며 “시간이 매우 오래 걸리는구나!”라고 소리친 후, 어떻게 해야 할지 깊은 고민에 빠질 것이다. 

100000
1 (10만개)
100000
0 0 99999 (10만개)

왜 시간이 오래 걸리는지는 간단히 생각해볼 수 있다. 우선 명령 수는 10만개이다. 간단히 Sequential Search(쭉 다 찾아보는 방법)을 이용한다면 한 개의 명령 계산만 해도 10만 번이 걸린다. 근데 명령 수는 10만개이다. 따라서 10만*10만>1억이므로 1초안에 계산이 될 리가 전혀 없다!

우리는 여기서 개선점이 필요함을 느꼈다. 어떻게 해야 할까? 바로 인덱스트리를 사용하는 것이다.(binary indexed tree는 합밖에 구하지 못한다.)

2. Indexed Tree

여기서부터는 프리젠테이션 파일을 참고하도록 하자.
2-1. 인덱스트리 개요
인덱스 트리가 완전히 구성된 1번 슬라이드를 참고하자. 제일 아래에 있는 2가 4와 비교하여 부모로 올라갔다. 이 연산엔 무슨 의미가 있을까? 부모노드는 모든 자식노드들의 값보다 같거나 작을 것이다. 따라서 일정 구간의 최솟값은 그 구간의 부모노드에 있을 것이다.

이해가 잘 안 갈수도 있으니 예제로 설명하겠다. “0 0 1”이라는 명령어를 받았다고 해보자. a[0]~a[1]의 최솟값을 찾으라는 연산이다. 다 찾을 수도 있지만, 그들의 공통 부모노드를 하나 찾으면 그걸로 끝이다. 따라서 2가 나올 것이다. 또 다른 명령어 “0 0 3”을 넣었다고 해보자. a[0]~a[3]이 포함된 공통 부모노드를 찾으면 역시 또 2가 나올 것이다.

2-2. 삽입 (insert(x,y) : x는 x번째에 y가 들어가야 한다는 것을 의미)
삽입은 제일 밑바닥(즉, leap node)에서부터 시작한다. x번째 leap node의 인덱스를 갖고 시작한다. 노드에 값을 갱신할 때에는 아래의 세 규칙을 따른다. I) 노드에 아무런 값도 없을 경우 : 값을 넣고 부모노드로 가고, 부모노드에 대해 재실시. II) 노드에 값이 있을 때 값이 작은 경우 : 값을 넣고 부모노드로 가고, 부모노드 재실시. III) II에 위배되는 노드이거나 값을 넣은 후 부모가 없을 경우 : 루프를 종료.
2-3. 대푯값 찾기 (find(sp,ep) : sp~ep를 대표하는 값을 찾는다.)
구간은 대표가 어떤 값이어야 하는가에 따라 융통성 있게 해주면 된다. 프리젠테이션을 참고하자.
2-4. 값 고치기 (insert(x,y), 삽입과 같이 그대로 써준다.)
삽입과 같다. 프리젠테이션을 참고하자.

이게 인덱스트리의 전부이다. 직접 구현을 해보도록 하자.

해보기)

3. Binary Indexed Tree

tree[i]

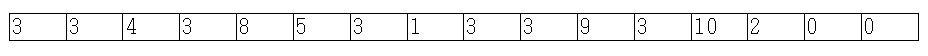
구성 훑어보기

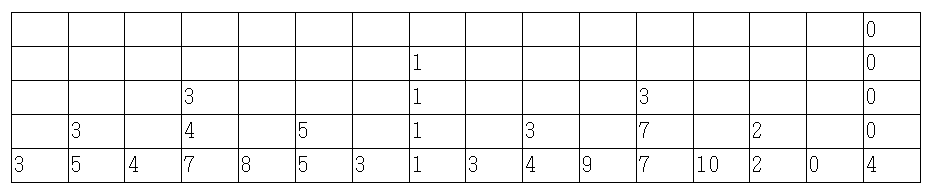
a[i]

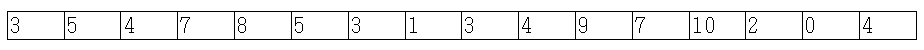
구간 최솟값을 구하는 BIT를 만들어보았다. 구성 훑어보기의 테이블을 보자. 더블릿의 한 유저는 저 테이블을 이해하지 못하여 “삼진트리가 되는데요?”라고 하였다. 그러나 다음 색칠한 것을 보게 되면 이진트리임을 알 수 있을 것이다.

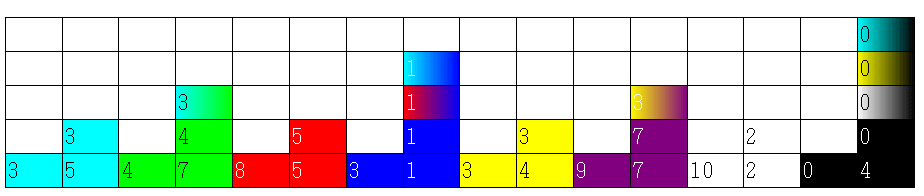
이 표를 보고도 이해가 안 간다고 생각된다면, 프리젠테이션을 참고하자.

Indexed Tree로 고쳐놓은 개형이 보인다. 그래도 이해가 안 간다고 생각되면, 손으로 위의 5*16 테이블을 그리고, Indexed Tree에서 어떻게 연결했는지 그대로 선을 그어보자. 그럼 “아하!” 소리치며 이해를 할 수 있을 것이다.

tree[i]

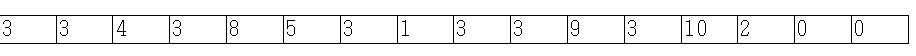
3-2. GET_LAST_BIT
BIT에서 올라가는데 있어 중요한 역할을 하는 함수이다. 자신의 위치의 인덱스 번호를 이진수로 바꾸었을 때, 마지막 비트를 얻어주는 역할을 해준다. 다음 함수를 기억하고, 구현할 때 사용하도록 하자. 
int GET_LAST_BIT(int x) {
   return x&-x;
}
3-3. read(x)
1~x까지의 대푯값을 찾는다. tree[x]부터 답을 계속 저장해둔다. 다음번 후보로 올라갈 때에는 x에 GET_LAST_BIT(x)를 빼주며 올라가면 된다. 그리고 x가 0이 되면 탐색을 종료한다. 
ex) read(13)
tree[13]->tree[12]->tree[8]->tree[0]=종료

ex2) read(15)
tree[15]->tree[14]->tree[12]->tree[8]->tree[0]=종료
탐색하면서 답이 될수 있는지 항상 체크를 해두어야 한다.

Q) read(x)는 1부터 답을 찾는다. 그렇다면 구간 합을 구하는 BIT에서 생각해보자. (x~y)를 BIT로 구현해보고자 한다. 어떻게 해야할까?

3-4. update(x,y)
x에 y를 넣는다. read와 반대로, GET_LAST_BIT(x)를 더해주면서 갱신해준다. 트리의 기준에 맞추어 융통성 있게 수행해주면 된다. 종료 조건은 범위를 넘을 때 종료한다. 
ex) update(1,10)
tree[1]->tree[2]->tree[4]->tree[8]->tree[16]->tree[32](범위 초과=종료)
ex2) update(3,0)
tree[3]->tree[4]->tree[8]->tree[16]->tree[32](범위초과=종료)
ex3) update(13,1)
tree[13]->tree[14]->tree[16]->tree[32](범위초과=종료)
3-5. 2D BIT
2차원으로 BIT를 구현한다. mobile문제 를 보도록 하자. 2D-BIT를 이용하면 되는 문제이다. 2D-BIT는 2차원적인 BIT로, tree[x][y]=(1~x),(1~y)를 대표할 수 있는 값을 찾을 수 있는 구조이다.

구성 방법은 간단하다. 우선 가로로 BIT를 만들어주고, 그것을 이용해 세로로도 BIT를 만들어주면 그게 2차원 BIT가 된다. update나 read 등의 함수도 1차원 BIT와 유사하게 하면 된다. 단, 가로 세로 모두 업데이트가 필요하니 주의하도록 하자.

written by victor5432

문서 II

우리는 종종 우리의 알고리즘을 더욱 빠르게 할 수 있는 자료구조가 필요하다. 이 문서에서 우리는 binary indexed tree 구조에 대해서 논의 해보자.

Peter M. Fenwick 에 따르면 이 구조는 처음 자료의 압축에 사용되어 졌다. 지금은 빈도수를 저장하고 저장된 빈도수 테이블에서 구간의 합을 구하는데 종종 사용되어 진다.

1. 문제 정의

여러개의 돌이 들어있는 n 개의 박스를 가지고 있다.

두가지 동작을 하는 경우

  1. 돌을 i 번째 박스에 더한다. --- update
  2. k 번째 박스에서 l 번째 박스까지의 돌의 합을 구한다. --- read

일반적인 해법은 질의 1 에서는 O(1) 에 , 질의 2 는 O(n) 에 가능하다. m 개의 질의가 주어진다면 최악의 시간복잡도는( 모두 2 번 질의 일 경우)는 O(n*m) 이 된다.

다른 접근 방법으로는 binary indexed tree 가 있다. 이 방법의 두가지 질의 모두 시간복잡도는 O(mlogn) 이다. 또한 코딩이 쉽다.

2. 개념 잡기

가정. ----

16 개의 원소를 가진 f[] 배열이 아래와 같다고 하자. ( 실제적으로 f 배열은 사용하지 않음... 설명을 위해서)

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
f[] 1 0 2 1 1 3 0 4 2 5 2 2 3 1 0 2

read,update 동작을 위해 실제적으로 tree[] 배열을 사용하고 , 각 트리 배열은 f[] 배열의 원소의 일부의 합을 저장하고 있다.

(1)read 동작

1 에서 13 번째 까지의 누적 합을 구하기 위해 tree[] 배열의 세 원소만 더하면 된다.

왜냐하면 을 가지고 있다.

- read 동작의 구현

1 부터 n 번째 원소까지의 누적합을 구하는 경우에 대해서 알아보자.

예를 들어 , 13 까지의 합을 구하는 경우 13 을 이진수로 표현하면

오른쪽에서 왼쪽으로 가다 최초로 0 이 아닌 자리를 알아내는 방법

a & -a
자세한 사항은 rms 문서를 참조

13 & -13 은 1 , 12 & -12 는 4 , 8 & -8 은 4 이다. 

int read(int idx)
{
   int sum = 0;
   while (idx > 0){
      sum += tree[idx];
      idx -= (idx & -idx);
   }
   return sum;
}

(2)update함수

n 번째 원수에 값을 더하거나 빼는 경우에 대해서 알아보자.

예로, 5 번째 원소의 값을 더하거나 빼는 경우 변경해야 할 원소는 5 , 6 , 8 , 16 이다.

read 함수는 빼가면 , update 함수는 더해가면 된다. 

int tree[20];
#define MaxVal 16
void update(int idx ,int val)
{
   while (idx <= MaxVal){
      tree[idx] += val;
      idx += (idx & -idx);
   }
}

3. 확장

(1) 2 차원 binary indexed tree

2 차원으로 확장하면 행 , 열의 원소가 일차원 binary indexed tree 처럼 움직인다.

소스--------- 

#define max_x 8
#define max_y 8

int tree[10][10];

int read(int x,int y)
{
   int sum;
   int y1;

   sum = 0;
   while (x > 0 ){
      y1 = y;
      while (y1 > 0 ){
         sum += tree[x][y1];
         y1 -= (y1 & -y1); 
      }
      x -= (x & -x); 
   }

   return sum;
}

void update(int x , int y , int val)
{
   int y1;

   while (x <= max_x){
      y1 = y;
      while (y1 <= max_y){
         tree[x][y1] += val;
         y1 += (y1 & -y1); 
      }
      x += (x & -x); 
   }
}

int main()
{
   update(1,1,10);
   update(1,2,5);
   update(2,1,4);
   update(2,2,3);
   update(1,1,10);

   printf("%d\n",read(2,2));
}
1,1 이 시작구간이 아니고,2 행 3 열 에서 4 행 5 열 사이의 합을 구하는 경우는
read(4,5) - read(1,5) - read(5,2) + read(1,2)
와 같이 구하면 된다. 일차원도 마찬가지이다. 
원문 : http://www.topcoder.com/tc?module=Static&d1=tutorials&d2=binaryIndexedTrees
[질/답]
[홈으로]  [뒤 로]
[푼 후(0)]