퇴각 검색(backtracking)

반복하는데 귀신인 컴퓨터에 적당한 방법이다. 가능한 경우를 모두 검사(exhaustive search)하는 무식한(?)방법이다.

답 내는 것이 문제가 아니라 얼마 만큼의 빠른 시간에 작업을 끝낼수 있는 가를 고민해야 되는 파트.

가능성이 없는 것은 미리 잘라버리는 것이 관건이다. 예를 들어, 3 번의 시합에서 2 번 우승하면 이기는 게임에서 미리 2 번 이기면 나머지 한 번은 할 필요가 없다. 이런 가능성을 생각해서 미리 많이 잘라버리면 그 만 큼의 실행시간이 빨라진다.

가능한 경우를 모두 검사하는 방법에는 보통 두 가지 유형의 문제로 나뉠수가 있다.

예를 들어 , 주머니 속에 7 개의 공이 있고 , 각 공에는 번호가 부여되어 있다.

부분집합형

주머니에서 몇 개의 공을 꺼내어 합이 13 이 공들을 찾는 경우에는 2^7 가지의 부분집합을 모두 검사해야 한다.

한 개 뽑는 경우

두 개 뽑는 경우 세 개 뽑는 경우 ...

7 개 모두 뽑는 경우

팩토리얼 형
7 개의 공을 임의로 나열했을 때 인접한 수의 곱이 최대 인 경우는 어떤 경우인가를 알고자 할 때 7! 가지의 모든 경우를 생각해야 하므로 이는 팩토리얼 형 문제라고 생각할 수 있다.

1. 부분 집합 형

주머니 속에 1,2,3 이 쓰져 있는 공 3 개가 있고 , 이를 뽑아내는 방법은 총 8 가지 경우가 있다.

모든 부분집합을 검사하는 경우의 문제이다. 즉 n 개의 원소를 가지는 집합의 부분 집합은 2^n 개이다. n 개의 원소가 존재하면 2^n 개 모두를 검사하는 방법이다. 물론 이 과정에서 답이 될 가능성이 없는 것은 미리 잘라내어 실행시간을 높인다. 
(문제) sum of subset 

6 , 1 , 9 , 8 , 3 , 4 , 7

총 합은 38 , 합은 반은 19 이다.

이 수들을 적절히 뽑아 19 를 만들 수 있는 방법의 수를 구하는 문제.

부분 집합형 문제의 기본 틀

첫째 원소, 둘째 원소 2 개 있을 때 부분집합의 수는 4 개이다. o 를 1 로 x 를 0 으로 놓으면 ,

원소의 수가 2 개 일 때

이를 구현하기 위해 배열(배열명을 include[] 라 하자)을 사용하여

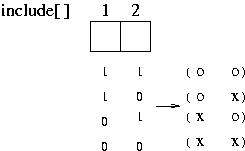
원소의 수가 3 개일 때

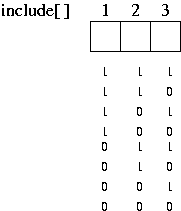
부분집합형 문제의 기본틀 

#include < stdio.h >
int include[5];
        
void bt(int i)
{
   int k;
      
   if(i==4){ 
       for(k=1;k<=4;k++)
          printf("%d ",include[k]);
          printf("\n");
   }else{
       include[i+1]=1; //포함하는 경우 
       bt(i+1);
       include[i+1]=0;//포함하지 않는 경우
       bt(i+1);
   }
}
        
main()
{
   bt(0);
}

(샘플 문제)수의 부분합 문제로 조금씩 실행 속도를 높여 보기로 하자. 문제는 전제 합의 반 50 이되는 원소를 골라내는 문제이다.
주어지는 데이터는 40 20 30 10 (수의 부분합 풀이)

(소스 1)

부분 집합형 기본 틀에서 포함하는 경우 즉 1 인 경우 에는 데이터를 더하면서 레벨을 높여가고 0 인 경우 더 하지 않고 가는 부분이 포함된 경우이다. 
int data[]={0,40,20,30,10};
int include[5];

void process(int i,int total)
{
  int k;

  if (i==4){
    if (total==50){
      for(k=1;k<=4;k++)
        if (include[k]==1) printf("%d ",data[k]);
      printf("\n");
    }
  }else{
    include[i+1]=1;
    process(i+1,total+data[i+1]);
    include[i+1]=0;
    process(i+1,total);
  }
}


main()
{
  process(0,0);
}
그림으로 나타내면

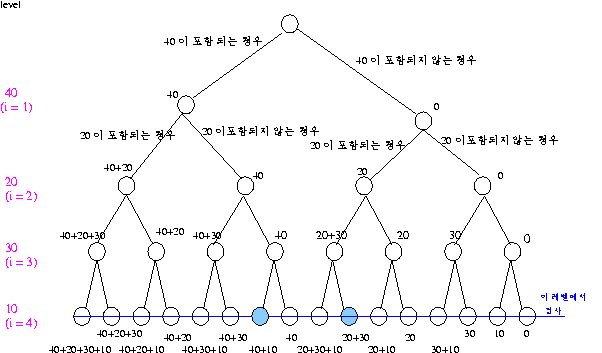
(소스 2)

소스 1 에서는 16 번의 비교가 일어난다.

소스 1 을 조금 더 개선해보면 , total 값이 구하고자 하는 50 을 초과하면 더 이상 의미가 없으므로 더 이상 확장하지 않으면 수행시간을 효율을 높일수 있을 것이다. 

int data[]={0,40,20,30,10};
int include[5];

void process(int i,int total)
{
  int k;

  if (total > 50) return; //이 부분 

  if (i==4){
    if (total==50){
      for(k=1;k<=4;k++)
        if (include[k]==1) printf("%d ",data[k]);
      printf("\n");
    }
  }else{
    include[i+1]=1;
    process(i+1,total+data[i+1]);
    include[i+1]=0;
    process(i+1,total);
  }
}

main()
{
  process(0,0);
}

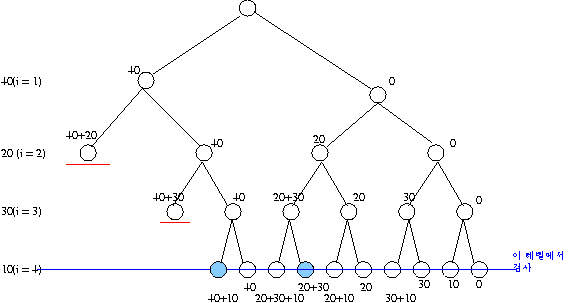
(소스 3 - bound 이용 )

i 번째 level 에서의 bound 값이란?
(i + 1 번째 데이터) + ( i + 2 번째 데이터) + ( i + 3 번째 데이터) + ....
문제에서 각 레벨 별 bound 값을 구하면

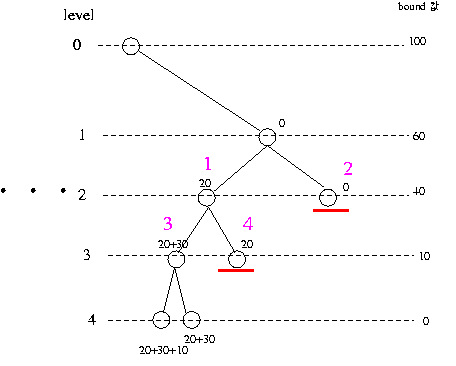
몇 지점에서 bound 에 대해 알아보면(합의 절반 50 을 구하는게 목표)

bound 를 이용하여 소스 2 를 조금 더 개선해보자. 

int data[]={0,40,20,30,10};
int include[5];

void process(int i,int total,int remaining)
{
  int k;


  if (total > 50) return;
  if (total+ remaining < 50) return; //이 부분 

  if (i==4){
    if (total==50){
      for(k=1;k<=4;k++)
        if (include[k]==1) printf("%d ",data[k]);
      printf("\n");
    }
  }else{
    include[i+1]=1;
    process(i+1,total+data[i+1],remaining-data[i+1]);
    include[i+1]=0;
    process(i+1,total,remaining-data[i+1]);
  }
}


main()
{
  process(0,0,100);
}

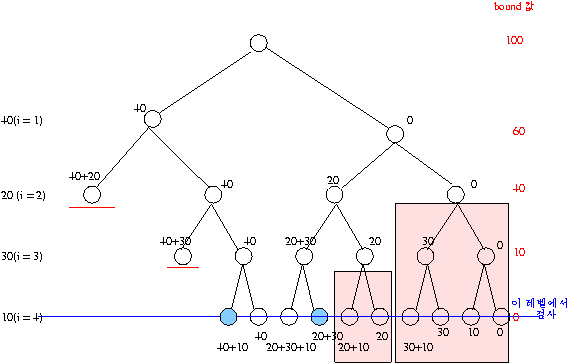
(소스 4)

소스 3 의 if 문을 함수로 띠어낸 형태 
int data[]={0,40,20,30,10};
int include[5];

int promising(int total,int remaining)  // 이 함수를 유망함수라 함 
{
  if (total > 50||total+ remaining < 50) return 0;
  return 1;

}

void process(int i,int total,int remaining)
{
  int k;

  if (promising(total,remaining))
     if (i==4){
       if (total==50){
         for(k=1;k<=4;k++)
           if (include[k]==1) printf("%d ",data[k]);
         printf("\n");
     }
   }else{
       include[i+1]=1;
       process(i+1,total+data[i+1],remaining-data[i+1]);
       include[i+1]=0;
       process(i+1,total,remaining-data[i+1]);
   }
}


main()
{
  process(0,0,100);
}
[질/답]
[홈으로]  [뒤 로]
[푼 후(0)]