Telephone Line Company(TLC)는 전화 케이블공사를 하고 있다. 그들은 1 에서 N 까지 붙여진 여러개의 지점을 서로 연결하고 있다. 두 지점은 같은 번호를 가질 수 없고 연결된 두 지점사이는 양방향 통화가 가능한다. 한 지역에서 모든 지역으로 통화가 가능하지만, 직접적으로 연결될 필요는 없교 다른 지역을 경유해서 가능하다.
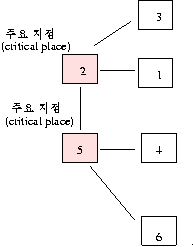
예를 들어, 기지국의 수가 6 개(1 , 2 ,..., 6)이고 2 번 기지국과 1,3 번 기지국이 직접 연결되어 있고, 5 번 기지국과 2,4,6 기지국이 직접 연결되어 있으면 , 주요 지점은 2 ,5 기지국으로 2 개이다.
때때로 전원장치에 이상이 생겨서 한 지역에 다른 지역으로 교환하지 못하는 경우가 발생한다. 이런 지점을 주요지점(critical place)이라 하고 , 우리가 해야 할 일은 이러한 주요지점의 수를 구하는 것이다.

적어도 한 기지국은 다른 기지국과 직접 연결되어 있다.
입력 5 5 1 2 3 4 출력 5 입력 6 2 1 3 5 4 6 2 출력 2 5
--무작정 하기 간단히 하는 방법은 모든 정점에 대해서 , 단절점을 검사하기 위해 검사할 정점에서 나가는 간선을 모두 없앤 후 , 정점에 연결된 정점에서 깊이우선탐색을 하여 모든 정점을 모두 방문가능하면 해당 정점은 단절점이 아니고 그렇지 않으면 해당 정점은 단절점이 된다. 예를 들어, 3 번 정점이 단절점이 되는 가를 보기 위하여 , 3 번 정점에 연결된 간선을 모두 제거한후 3 번 정점에 연결된 2 번 혹은 4 번 정점에서 깊이우선탐색을 해서 모든 정점을 방문가능하면 이 점은 단절점이 아니다. 3 번 정점은 단절점이 아니다. 4 번 정점이 단절점인가를 확인하기 위해 , 4 번 정점에 연결된 모든 간선을 제거한 후 4 번 정점에 연결된 정점 1 , 3 , 5 , 6 , 7 번 정점 중 한 정점에서 깊이우선탐색을 하면 4 번 정점은 단절점이란 것이 쉽게 나타난다.
한 정점이 단절점인가를 알기위해 정점마다 깊이우선탐색을 수행해야 하므로 정점의 수가 많은 경우에는 효율이 떨어진다. 이는 다음에 알아보는 방법을 통해 실행속도를 빠르게 할 수 있다.
빠르게 하기
먼저 , 트리간선(tree edge)과 백 간선(back edge) 이란 용어에 대해서 알아보면 , 트리 간선이란 연결된 그래프가 주어질 때 트리를 만들기에 필요한 간선을 트리 간선이라하고, 남은 간선을 백 간선이라 한다. 아래 그림은 0 번 정점을 시작정점으로 하여 깊이우선 탐색을 하였을 때의 트리 간선과 백 간선이고 그림. 다 는 이를 정리한 그래프이다. 점선은 백 간선을 의미한다. low 값이란?아래 세 값중 최소가 정점 u 의 low 값이다.단절점 조건?
- 정점 u 의 깊이우선탐색시 방문 순서, dfn(u)
- 정점 u 의 자식 노드중 가장 적은 low 값
- 정점 u 의 백 간선의 dfn 값
정점 u 가 단절점이 되는 조건은 루트노드일 때는 u 의 자식 노드가 2 개 이상이면 u 는 단절점 루트노드가 아닌 경우 dfn(u) 와 정점 u 의 자식 중 한 자식이라도 dfn(u)보다 low 값이 크거나 같으면 정점 u 는 단절점이 된다.
소스 설명.void dfnlow(int u,int v){ // u 가 자식(4) , v 가 아버지(2) int j; dfn[u]=low[u]=num++; for(j=0;j < n;j++) if (matrix[u][j]==1){ if ( dfn[j] < 0) { // u 에 연결된 정점 중 방문되지 않는 j dfnlow(j,u); //재귀 호출 , j 는 자식 u 는 아버지 low[u]=low[u] < low[j] ? low[u] : low[j]; }else // u 에 연결된 정점 중 방문된 j 중 if ( j != v) low[u]= low[u] < dfn[j] ? low[u]:dfn[j]; //back edge } }소스출처:acm 참조:fundamental datastructures in c// 테스트 데이터가 빈약 함.