1. AOE(Activity On Edge) network
(문제1) 아래 그림은 볼트 ,너트를 만든 후 두 개를 조립하는 단계를 보여주는 그래프이다.
동시 작업이 가능하다고 한다면 완성된 부품을 만드는데 걸리는 시간은 얼마인가?
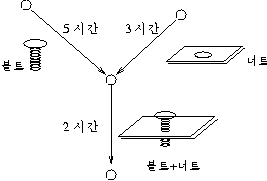
(문제 2)여유인력이 있다면 어떤 작업에 투입하면 전체적인 작업시간을
단축할 수 있을 까?
AOE 네트워크는
간선(edge)이 작업을 나타내고 ,
정점이 작업의 종료를 나타낸다.
이 네트워크의 주 관심사는 어떤 작업에 투자(투입)해야 전체적인 작업 시간을 단축하느냐
이다.
- 임계 경로(critical path)란?
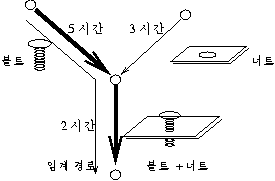
가장 많은 시간이 걸리는 길을 임계 패스(critical path)라 한다. 위 보기 에서는 볼트 만들고 ,
(볼트+너트) 조립하는 길이 임계 패스가 된다. 작업시간을 단축하기 위해서는 임계 패스에
투입하면 작업시간을 단축할 수 있다.
- 임계 경로 크기(critical path length)란?
임계 경로상의 있는 시간의 합
- 가장이른 시간(earliest time)과 가장 늦은 시간(latest time)란?
너트는 기다림없이 바로 작업을 시작할 수 있으므로 early(너트)=0 이고 , 너트 만드는
작업은 2 시간이후에 시작해도 하나를 만드는 전체적인 작업시간은 영향이 없으므로
late(너트)=2 이다.
early(볼트+너트)는 5 시간 이후에는 시작할수 있고 , late(볼트+너트) 도 5 시간 이후에는
시작해야 전체적인 작업시간이 늦어지지 않는다. 따라서 임계경로 상의 early ,late 시간은
항상 동일하다.
(손으로 푸는 문제)
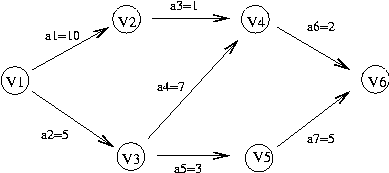
- 임계 경로?
- 임계 경로 크기?
- a5 번 작업의 early,late 시간
2. 구현(임계 경로를 구하는 방법)
시작 정점에서 DFS 로 접근. 정점에 도착후
- indegree 를 감소 ,
- 가지고 있는 패스 크기와 지금의 패스크기를 비교 후
지금의 패스 크기가 커다면 갱신
- 정점의 Indegree 가 0 이면 DFS , 아니면 return
위 문제에서는
- 1 번 정점에서 DFS
- 2 번 정점의 indegree 를 1 감소하면 0 이므로
- 2 번 정점에서 4 번 정점으로 4 번 정점의 indegree 를 1 감소. 그런데
4 번 정점의 indegree 가 2 에서 하나 감소하면 1 이 되므로 리턴.
(4 번 정점의 indegree 가 0 이 아니란 것은 아직 4 번 정점으로 오는 길이
있다는 의미이므로 , 다른 길로 4 번 정점에 올때 까지 4 번 정점으로 오는
길이 최대가 아닌지를 최종적으로 판단하지 못한단다는 것)
3. 시간 복잡도
출처:dovelet



