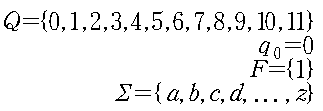KMP 알고리즘에 대해서

1. 문자열 탐색

기본적으로 우리는 문자열에서 문자를 찾는 알고리즘을 짠다면 하나씩 다 찾게 만드는 것이 대다수일 것이다. 만약 우리가 "abcababcabc"에서 “abc”라는 문자열을 찾을려고 할 때, 우리가 소스를 짠다면 이런 형태일 것이다.

#include <stdio.h>
#include <string.h>

int main()
{
   char s[1000]={0},p[100]={0};
   int i,j,slen,plen;
   bool check;
   scanf("%s",s);
   scanf("%s",p);
   slen=strlen(s),plen=strlen(p);
   for(i=0;i < slen-plen+1;i++)
   {
      check=true;
      for(j=i;j < i+plen;j++)
      {
         if(s[j]!=p[j-i])
         {
            check=false;
            break;
         }
      }
      if(check) printf("Match : %d to %d\n",i+1,i+plen);
   }
   return 0;
}

<보기 1> 원시적인 문자열 탐색 알고리즘

이렇게 소스를 짠다면 문자열 s,p 에 대해 문자열의 길이를 m,n이라고 한다면 총 수행 시간은 Θ(mn)의 시간이 걸릴 것이다. 이는 문자열의 길이가 길수록 매우 비효율적이다. 그렇다면 이제부터 더욱 빠르게 탐색하는 KMP 알고리즘에 대해 알아보자

2. 오토마타를 이용한 문자열 탐색

위에서 본 원시적인 방법을 더욱 빠르게 하기 위하여 오토마타를 사용해보자. 일단 오토마타를 모르는 사람들도 있을테니 dovelet 30장에서도 알아보겠지만 간단하게 설명하겠다. 오토마타는 여러 가지의 상태로 표현되는데, 문제 해결 절차를 상태의 변화로 표현하는 것이다. 오토마타는 다음과 같은 구성요소로 이루어져있다.

자, 이제부터 소스를 작성해보자. 일단 우리가 어떤 알파벳으로 이루어진 문자열에서 abcdeabcade라는 문자를 찾는다고 하면, 이와 같이 오토마타를 만들어낼 수 있다.

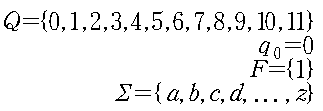
우리가 “abcdeabcade"에서 하나도 진행 안된 상태를 0, ”a"까지 했을 때 1, “ab"까지 했을 때 2, ... , 전체를 다 했을 때 11이라고 하면, 상태 전이 함수 δ는 다음과 같이 정의된다

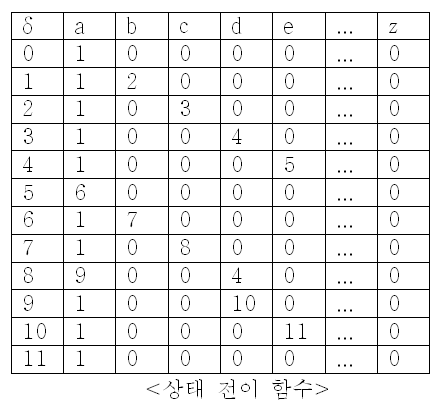
헌데, 어째서 상태 8에서 d를 입력받으면 4로 넘어가는 것일까? 하는 분들도 계실 것이다. 만약 이게 없다면 오토마타를 만든 이유가 없다. 우리가 상태 8에 있다는 것은 문자열에서 “abcdeabc"까지 일치했다는 소리다. 그런데 그 다음에 d가 나오면 "abcdeabcd"가 되므로 상태 9로 넘어갈 수는 없지만, 뒤의 ”abcd"가 있으므로 상태 4로 넘어갈 수 있는 것이다. 이것으로 오토마타는 완성되었다.

이러한 오토마타를 완성했다면 소스를 이렇게 짤 수 있을 것이다. (s는 전체 문자열,p는 탐색할 문자열, f는 목표 상태, slen은 s의 길이, plen은 p의 길이)

Matcher()
{
   int q=0,i;
   for(i=0;i < slen;i++)
   {
      q=δ(q,s[i]);
      if(q==f) printf("Matched!");
   }
}

이 얼마나 간단해지는가? 하지만 더욱 간단하게 할 수 있다. "abcdeabcade"를 보면, 사용된 문자는 a, b, c, d, e 뿐이다. 고로 나머지 문자는 ‘기타’ 항목으로 넣어버릴 수 있다. 고로 아래와 같이 문자로 테이블을 만들어서 문자를 숫자로 변환시킨 후 더욱 간단하게 할 수 있다.

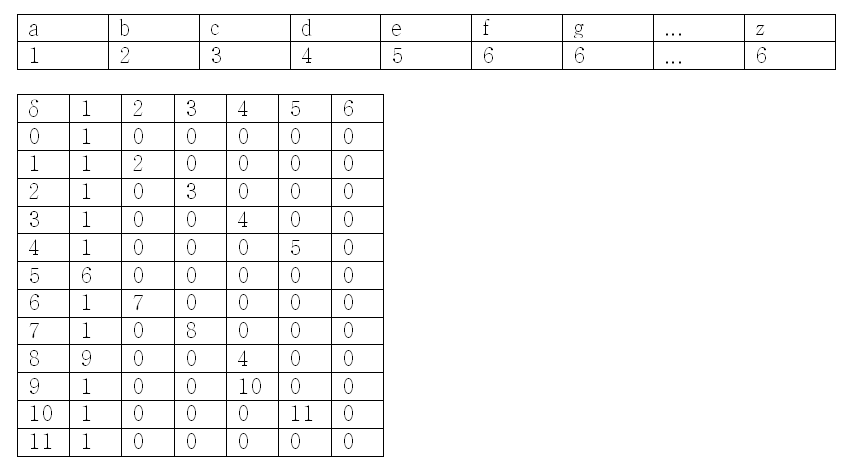
3. KMP 알고리즘

우리는 오토마타를 이용하여 간단하게 만들어 보았다. KMP 알고리즘은 크누스(Knuth), 모리스(Morris), 프랫(Pratt) 세 사람의 이름을 딴 알고리즘으로, 위의 오토마타 문자열 탐색 알고리즘과 비슷하나, 상태 전이 함수 δ처럼 복잡하지 않고 더욱 간단명료하며 속도도 더욱 빠른 것이 특징이다. KMP 알고리즘에서는 δ대신 π를 이용한다.

만약 우리가 “abcdabcwz”라는 문자열을 어떤 문자열에서 찾는다고 하자. 만약 우리가 어떤 문자열에서 탐색을 하다가 “abcdabc"까지 일치했는데 다음에 d가 나왔다면? 오토마타에서처럼 바로 ”abcd"까지 일치된 상태로 바꿔버릴 것이다.

자, 이렇게 7번째까지 맞았는데 8번째 문자에서 틀렸다면? 그렇다면 그 다음에는 4번째 문자 ‘d'와 비교를 하게 만든다. 이렇게 하는 배열이 바로 π이다. 배열 π는 문자열을 탐색할 때 틀렸으면 다음으로 검색할 문자의 인덱스를 알려준다. “abcdabcwz"를 탐색할 때 π[7]은 3과 같아진다 (8번째 문자와 비교한 후 4번째 문자와 바로 비교하므로). 그렇다면 ”abcdabcwz"에 대해 π는 이렇게 작성할 수 있다.

(π[0]의 경우 -1로 처리한 경우는 ‘예외 처리’를 위해서 한 것이다. 절대 -1번째 주소값을 찾게 만드는 것이 아니다.)

자, 이제 소스를 보자.

#include <stdio.h>
#include <string.h>

char s[1000]={0},p[100]={0};
int n,m,pi[100]={0};
void find_pi()
{
   int i=0,j=-1;
   pi[0]=-1;
   while(i < m)
   {
      if(j==-1 || p[i]==p[j])
      {
         i++,j++;
         pi[i]=j;
      }
      else j=pi[j];
   }
}
void kmp()
{
   int i=0,j=0;
   while(i < n)
   {
      if(j==-1 || s[i]==p[j]) i++,j++;
      else j=pi[j];
      if(j==m)
      {
         printf("Match : %d to %d\n",i-m+1,i);
         j=pi[j];
      }
   }
}
int main()
{
   scanf("%s",s);
   scanf("%s",p);
   n=strlen(s),m=strlen(p);
   find_pi();
   kmp();
   return 0;
}

자, 이것으로 KMP 알고리즘이 완성되었다. KMP 알고리즘의 총 수행 시간은 Θ(n)이다.

출처:jhs7jhs